Números de Fibonnacci

Los números de Fibonnacci siguen la conocida recurrencia:

\[ F_n = F_{n-1} + F_{n-2} \]

Empezando con 0, 1 obtenemos:

\[ 0, 1, 1, 2, 3, 5, 8, \ldots \]

Esta sucesión tiene algunas propiedades curiosas:

• El MCD de dos números de Fibonacci es otro número de Fibonacci: \(\mathrm{mcd}(F_n, F_m) = F_{\mathrm{mcd}(n, m)}\)

• \(F^2_{n+1} + F^2_{n} = F_{2n+1}\)

• \(F_n = \frac{F_{n-2} + F_{n+1}}{2}\)

Leonardo de Pisa, conocido como Fibonacci (filius Bonacci) fue un matemático italiano del siglo XII, originario de Pisa.

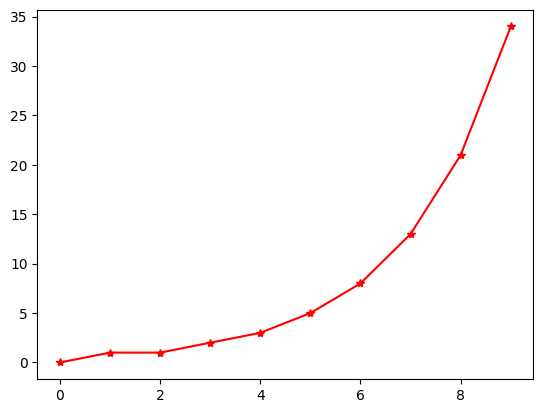
import matplotlib.pyplot as plt

def fib(n: int):
    """Fibonacci number n
    
    Naive recursive inplementation of Fibonacci number n
    Do not use for large numbers.
    
    First 7 terms of the series:
    [0,1,1,2,3,5,8]
    """
    if n == 0:
        return 0
    if n == 1:
        return 1
    return fib(n-1) + fib(n-2)

ns = range(10)
fibs = [fib(i) for i in ns]

plt.plot(ns, fibs, 'r*-')

[<matplotlib.lines.Line2D at 0x7f0e53ed4a50>]