Números de Fibonnacci complejos

Los números de Fibonnacci siguen la conocida recurrencia:

\[ F_n = F_{n-1} + F_{n-2} \]

Empezando con 0, 1 obtenemos:

\[ 0, 1, 1, 2, 3, 5, 8, \ldots \]

La secuencia puede extenderse hacia enteros negativos reordenando la relación de recurrencia:

\[ F_{n-2} = F_n - F_{n-1} \]

Con lo que obtenemos la secuencia:

\[ 0, 1, -1, 2, -3, 5, -8, \ldots \]

Con lo que se cumple:

\[ F_{-n} = (-1)^{n+1} F_{n} \]

Para extender los números de Fibbonacci al campo real, podemos utilizar la fórmula de Binet, que nos permite obtener el n-esimo término sin recurrencia:

\[ F_n = \frac{\phi^n - (1 - \phi)^n}{\sqrt{5}} \]

y donde \(\phi = \frac{1 + \sqrt{5}}{2}\)

Sin embargo, como \(1 - \phi\) es negativo, esta relación solo devuelve resultados reales para los números enteros.

No podemos obtener números de Fibbonacci reales, pero sí complejos.

import numpy as np
import matplotlib.pyplot as plt
import math

SQRT5 = math.sqrt(5)
PHI = (1 + SQRT5) / 2

def fibbn(n):
    """ Fibonacci numbers via Binet formula"""
    return (PHI**n - (1-PHI)**n)/SQRT5

# Complejos, parte real y parte imagianria

xx = np.linspace(0, 4, 1000)
zz = xx + 1j * 0
ii = np.arange(0, 5)

# Complejos
cfib1 = fibbn(zz)
# Enteros
ifib1 = fibbn(ii)
    
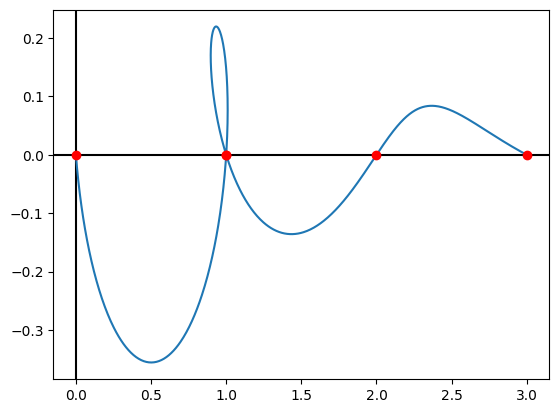
plt.axhline(y=0, color='k')
plt.axvline(x=0, color='k')
plt.plot(cfib1.real, cfib1.imag)
plt.plot(ifib1, [0 for f in ifib1], "ro")
plt.show()
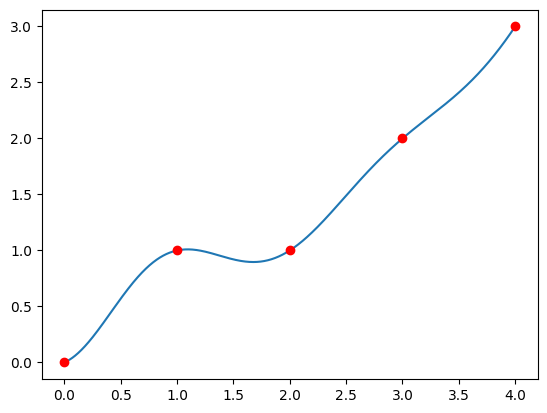
plt.plot(xx, cfib1.real)
plt.plot(ii, ifib1, "ro")
plt.show()
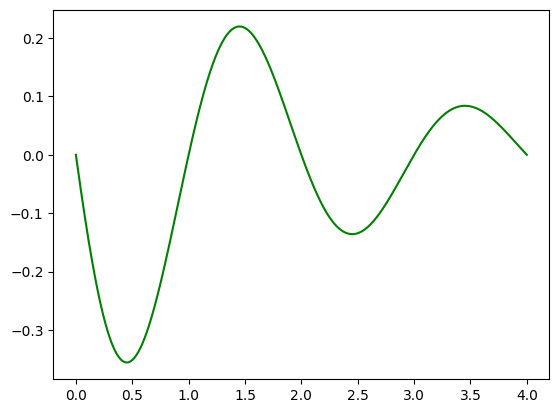
plt.plot(xx, cfib1.imag, 'g')
plt.show()

def plot_fibb1(n1=0, n2=4):
    xx = np.linspace(n1, n2, 1000)
    zz = xx + 1j * 0
    ii = np.arange(n1, n2 + 1)

    cfib1 = fibbn(zz)
    ifib1 = fibbn(ii)

    plt.axhline(y=0, color='k')
    plt.axvline(x=0, color='k')
    plt.plot(cfib1.real, cfib1.imag)
    plt.plot(ifib1, [0 for f in ifib1], "ro")
    plt.show()
    plt.plot(xx, cfib1.real)
    plt.plot(ii, ifib1, "ro")
    plt.show()
    plt.plot(xx, cfib1.imag, 'g')
    plt.show()

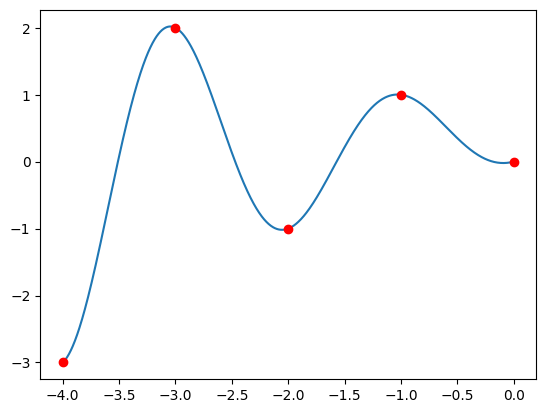
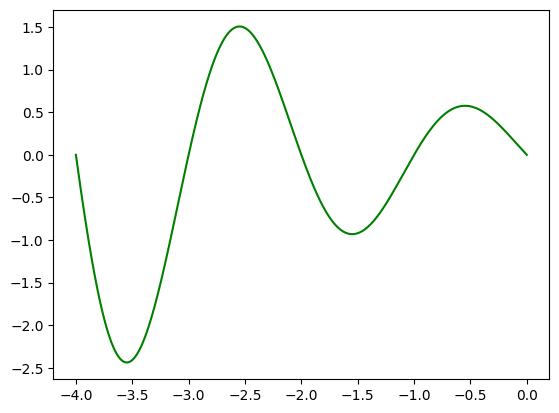
plot_fibb1(-4, 0)

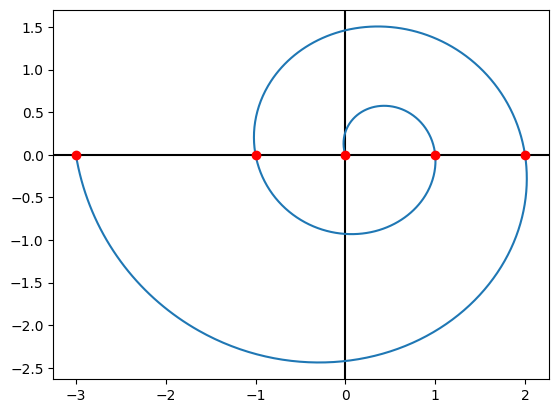
Con widgets

Cargamos el módulo ipywidgets y utilizamos la función interact

from ipywidgets import interact
import ipywidgets as widgets

# interact crea controles a partir de los argumentos
# de la función. Para cada tipo de argumento (entero, cadena)
# crea un control diferente
# Utiliza los valores por defecto como valores iniciales
interact(plot_fibb1, n1=(-5, 5), n2=(0, 5));

def plot_fibb2(n1=0, n2=4):
    
    # definitions for the axes
    left, width = 0.1, 0.65
    bottom, height = 0.1, 0.65
    spacing = 0.005

    rect_scatter = [left, bottom, width, height]
    rect_histx = [left, bottom + height + spacing, width, 0.2]
    rect_histy = [left + width + spacing, bottom, 0.2, height]

    fig = plt.figure(figsize=(8, 8))

    ax1 = fig.add_axes(rect_scatter)
    ax2 = fig.add_axes(rect_histx, sharex=ax1)
    ax3 = fig.add_axes(rect_histy, sharey=ax1)
    
    xx = np.linspace(n1, n2, 1000)
    ii = np.arange(n1, n2 + 1)
    cfib1 = np.array([fibbn(x+ 1j*0) for x in xx])
    ifib1 = np.array([fibbn(i) for i in ii])
    
    ax1.plot(cfib1.real, cfib1.imag)
    ax1.plot(ifib1, [0 for f in ifib1], "ro")
    
    ax2.plot(cfib1.real, xx)
    ax2.plot(ifib1, ii, "ro")
    ax2.tick_params(axis="x", labelbottom=False)
    
    
    ax3.plot(xx, cfib1.imag)
    ax3.tick_params(axis="y", labelleft=False)

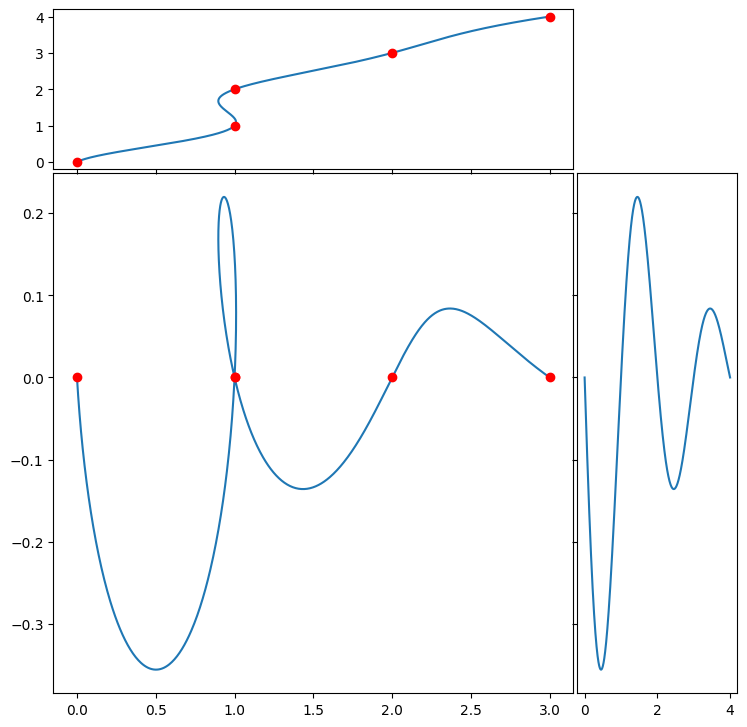
plot_fibb2()

interact(plot_fibb2, n1=(-7,0), n2=(0,7));

# En el caso de un gráfico, se actualiza para
# cada movimiento de los controles
# se puede evitar con `continuous_update=False`
# pero tenemos que crear los controles explícitamente
interact(plot_fibb2, 
         n1=widgets.IntSlider(min=-7, max=0, value=0, 
                              continuous_update=False),
         n2=widgets.IntSlider(min=0, max=7, value=4,
                              continuous_update=False)
        );